BOJ 1309 (동물원)
풀고나서 확인해보니, 훨씬 짧은 코드로 푸는 방법이 있어서 놀랬던 문제다.
우선 2 x N 타일링 문제처럼 가능한 방법들을 그려놓고 분할해서 생각하려고 노력했다.
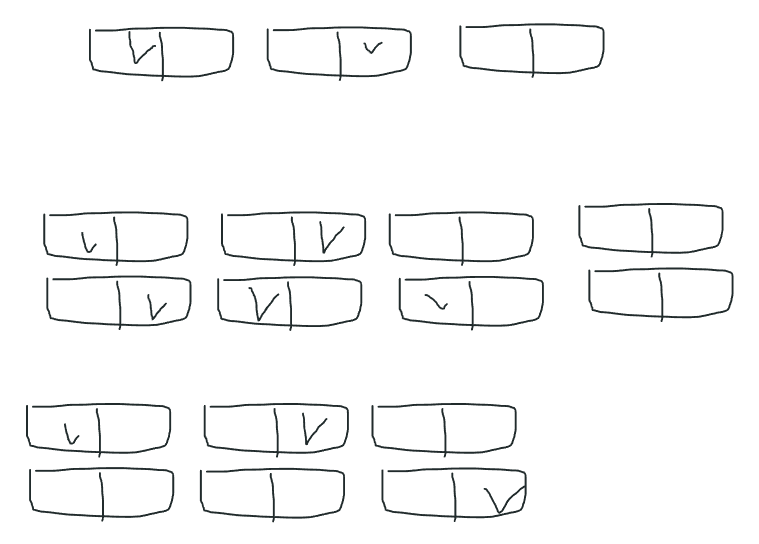
2 x 1일때 가능한 배치 방법은 3가지이다.
- 왼쪽에 배치
- 오른쪽에 배치
- 배치하지 않음
이걸 잘 기억해서 2 x 2일때 가능한 방법을 그려보면, 이런 규칙이 보인다.
- n번째 칸에서 왼쪽에 배치할 수 있으려면, n-1번째 칸에서는 오른쪽에 배치했거나 배치하지 않았어야 한다. (2가지)
- n-1번째 칸에서 오른쪽에 배치했던 가짓수랑 배치하지 않았던 가짓수를 더해줘야함.
- n번째 칸에서 오른쪽에 배치할 수 있으려면, n-1번째 칸에서는 왼쪽에 배치했거나 배치하지 않았어야 한다. (2가지)
- n-1번째 칸에서 왼쪽에 배치했던 가짓수랑 배치하지 않았던 가짓수를 더해줘야함.
- n번째 칸에서 배치하지 않으려면 n-1번째 칸에서 어떻게 배치했었던간에 상관 없다. (3가지)
- n-1번째 칸에서 왼쪽에 배치했던 가짓수, 오른쪽에 배치했던 가짓수랑 배치하지 않았던 가짓수를 더해줘야함.
따라서 각 상태에 대한 가짓수를 메모하는 배열을 세우고, n-1에서의 가짓수를 더해주면서 올라가면 된다.
D[N][0] = 이번 칸에 배치하지 않는 가짓수
D[N][1] = 이번 칸에서 왼쪽에 배치하는 가짓수
D[N][2] = 이번 칸에서 오른쪽에 배치하는 가짓 수
이 문제에서 주의할 점은 각 계산마다 지정된 MOD값(9901)으로 나누어주면서 처리해야된다는 것이다.
내가 세운 코드는 다음과 같다.
D[1][0] = 1;
D[1][1] = 1;
D[1][2] = 1;
int total = 0;
for(int i = 2; i <= n; i++) {
D[i][0] = D[i - 1][0] + D[i - 1][1] + D[i - 1][2];
D[i][1] = D[i - 1][0] + D[i - 1][2];
D[i][2] = D[i - 1][0] + D[i - 1][1];
D[i][0] %= MOD;
D[i][1] %= MOD;
D[i][2] %= MOD;
}
total = D[n][0] + D[n][1] + D[n][2];
System.out.println(total%MOD);
이렇게 해서 아주 빠르게 통과할 수 있었다.
사실 처음에는, 배치하는 가짓수를 N=1부터 N=4까지 직접 찾아본 다음에 규칙을 찾아보려고 했으나.. 잘 안되었고 점화식을 잘 세워서 DP로 푸는게 좋겠다는 결론을 내림 ㅠㅠ
예전이었으면 이런 문제에 대해서 아예 감을 잡지 못했을 건데 지난 오프라인 강의 첫 수업에서 배운 것들이 아주 크게 도움되고 있다.