BOJ 1068 - 트리
9월에 이 문제를 풀려고 시도했다가, 꽤 많이 틀리고 보류했었다.
오늘 기존에 작성했던거 다 지우고 새로 짜서 결국 맞았는데 너무 쉬운 부분을 놓치고 있었다는 생각이 든다.
트리에 대해 이론만 공부했을 때 풀어보면 좋은 문제라고 생각.
접근 방법
처음에는 이 문제를 배열로만 해결하려고 생각했었다.
거의 다 푼 것 같았는데 예외 처리를 못했는지 계속 런타임 에러가 나거나 틀리는 일이 발생했고, 이번에 풀 때는 그래프로 만들어서 풀어버렸다.
(나중에 맞은 사람 코드를 보니 충분히 배열로 가능했다)
내가 접근한 방식은 아래와 같다.
- 인접 리스트에 입력 받은대로 노드를 삽입
tree[i]의 부모값으로 i-1이 입력되었다고 치면graph.get(i-1).add(i)이런 식으로.
- 각 노드별로 한번씩 탐색해서 graph size가 0인 경우 리프 노드 count 해줌
- removeNode 입력 받은 것을 기반으로 DFS 돌려줌
- 자식 노드 탐색해서 해당 노드의 graph size가 0인 경우 아까 구했던 리프 노드 count 감소
- removeNode의 부모가 오직 removeNode만 자식으로 가지고 있었을 경우, 이 경우는 count 감소에서 제외해야함
여기서 핵심은 removeNode의 부모가 오직 removeNode만 자식으로 가지고 있는 경우이다.
다음 그림을 살펴보자.
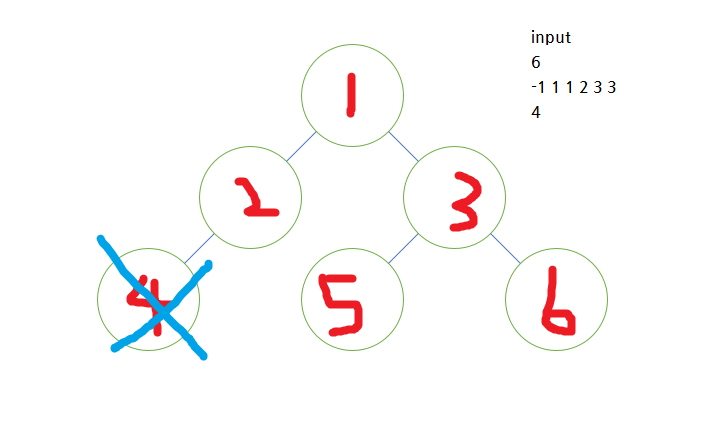
트리가 이런 식으로 있는 상태에서, 입력받은 removeNode 값이 4라고 치자.
그럼 4번 노드가 리프 노드이기 때문에 리프 노드의 count가 1 감소하고, 부모 노드였던 2번 노드가 자식이 없어지면서 리프 노드가 되어버린다.
따라서 답은 3이 나와야 하는데 (리프 노드 2, 5, 6) 예외 케이스를 처리 안해주면 2가 나올 것이다.
이 문제가 틀리기 쉬운 이유는 두 가지가 있는데..
1) 입력받은 노드 처리한 이후에 부모 노드가 리프 노드로 바뀌는 사태에 대비하지 않음
2) 루트 노드가 항상 0이 아니라는 점을 고려하지 않음
이정도인 것 같다.