BOJ 10986 - 나머지 합 (https://www.acmicpc.net/problem/10986)
처음에 너무 어렵게 생각해서 접근을 잘 못하고, 며칠정도 느긋하게 고민하다가 풀었다.
누적합 관련해서 이미 여러 문제를 풀어봤지만.. 좀 색다른 느낌이어서 재밌었다.
접근 방법
잘하시는 분들이 써놓은 공식? 증명? 같은거 너무 어렵다. ㅠㅠ 일단 다음 입력에 대해 누적합을 구해보자.
N = 5, M = 3
1 2 3 1 2
---------
1 3 6 7 9 -> 누적합
각 누적합에 대해 M으로 나눴을 때의 나머지를 구해보자.
1 2 3 1 2
---------
1 3 6 7 9 -> 누적합
---------
1 0 0 1 0 -> 3으로 나눈 나머지
어떤 구간을 M으로 나눴을 때 0이 되는 경우 count에 포함시키면 되는 간단한 문제라고 생각했지만, 여기서부터 생각이 막히기 시작했다.
(여기부터 편의상 시작 index를 0이 아니라 1이라고 쓰겠다)
누적합에 대한 나머지를 들여다보면서 조건에 해당하는 구간이 몇개 있는지 손으로 직접-_- 구해보면 한 가지 사실을 발견할 수 있는데, (1, a) 구간과 (1, b) 구간의 나머지가 같은 경우 (a+1, b) 구간은 나누어 떨어지는 구간이라는 것이다.
예를 들어 위의 입력 예시에서 (1, 1) 구간은 3으로 나눈 나머지가 1이다. (1, 4) 구간도 나머지가 1이다.
그리고 (1, 4) 구간에서 맨 앞 1을 제외한 (2, 4) 구간은 2 + 3 + 1 = 6, 6 % 3 = 0
사실 여기까지 구하고 나서도 그런 생각이 들었다. ‘그래서 어쩌라고? count 구하려면 결국 어떻게 해야되는건데?’
그래서 결국 손으로 직접-_- 구해보면서 규칙을 찾았다.
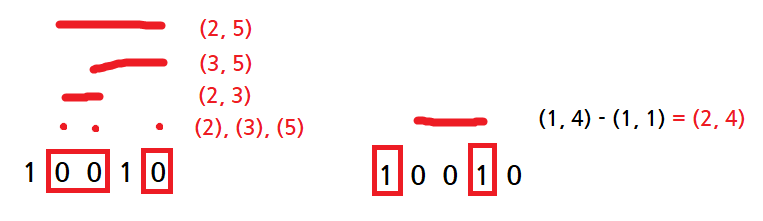
대충 이런 그림이 나온다.
- 나머지가 0인 구간을 n이라고 했을 때, 나누어 떨어지는 구간 개수는 n * (n+1) / 2 이다.
- 나머지가 0이 아닌 구간을 m이라고 했을 때, 나누어 떨어지는 구간 개수는 m * (m-1) / 2 이다.
- m이 1이면 나누어 떨어지는 구간 개수는 그냥 0개다. 자기랑 똑같은 나머지를 갖고 있는 구간이 한 개는 더 있어야 나누어 떨어지는 구간을 만들어낼 수 있으니까. (나머지 0이면 이거는 해당 안됨)
그럼 우리가 해야할 일은 나머지가 같은 구간이 몇개 있는지 세어줄 count 배열을 하나 만들어주고, 그걸 이용해서 답을 구하면 된다. 다행히 이 문제는 M제한이 1000 밖에 안되는지라 공간도 별로 안잡아먹는다.
그리고 나중에서야 깨달은 사실이지만 n개의 숫자를 굳이 배열에 담아놓을 필요는 없다. 어차피 누적합이랑 나머지를 구하고 나면 그 배열은 전혀 쓸모가 없다.
int prefix = Integer.parseInt(st.nextToken()) % m;
count[prefix]++;
for(int i = 1; i < n; i++) {
prefix = (prefix + Integer.parseInt(st.nextToken())) % m;
count[prefix]++;
}
long ans = count[0] * (count[0]+1);
for(int i = 1; i < m; i++) {
if(count[i] != 0) {
ans += count[i] * (count[i] - 1);
}
}
System.out.print(ans / 2);
사소한 팁을 추가하자면, 결과값에 구간 개수 더해줄 때 일일히 2로 나누지 말고 마지막에 출력할 때만 나눠주면 된다. 어차피 똑같으니까… 딴 블로그는 문제 풀이 설명 잘해주시는데 난 이런거 설명 잘 못하는거 같다. ㅠㅠ