Joshua Blog

[프로그래머스] 레벨 3 - 경주로 건설

Mar 20, 2021
3 minute read

프로그래머스 레벨 3 - 경주로 건설 (https://programmers.co.kr/learn/courses/30/lessons/67259)

오늘은 프로그래머스 스킬 체크 레벨3에 도전해봤는데, 다행히 한 번 만에 시간내로 통과할 수 있었다.

lv3

레벨3 문제 중에서 줄 서는 방법이랑 경주로 건설이 나왔는데, 이 중 경주로 건설 문제는 정말 재밌게 풀 수 있었다. 그래서 한 번 풀이를 적어보려고 한다.

풀이

최단거리가 아닌, 최소 비용을 구해야한다는 특성 때문에 DP 문제라 판단하고 접근했다.

탐색하는 방법으로는 이전에 비슷한 문제를 풀 때 DFS를 사용했기 때문에 이 것도 DFS를 사용했고, 생각보다 엄청 편하게 문제를 풀 수 있었다 😀

풀이 방법은 (0, 0) 좌표에서 시작해서 열심히 DFS를 돌려주고, 도로 짓는 비용을 계산하여 각 좌표별로 그때까지의 최소 비용을 기록해주면 된다.

따라서 최소 비용을 기록할 DP 배열과, 방문 여부를 기록할 visit 배열이 필요하니 잊지 말고 만들어주도록 하자.

그리고 이 문제의 경우 DFS 과정에서 필요한 메서드가 2가지 있는데, 아래를 참고하자.

  • 해당 좌표로 이동 가능한 지 확인하는 메서드
  • 현재 좌표 <-> 해당 좌표 간 도로 건설 비용 계산 메서드

첫번째 메서드의 경우, DFS를 사용하는 기본적인 문제를 몇 번 풀어봤다면 충분히 생각할 수 있는 로직이니 자세히 설명하지는 않으려고 한다.

두번째 메서드는 조금 막막하게 느껴질 수 있는데, 직전 방향을 기억할 수 있도록 재귀 함수를 구성하면 그리 어렵지 않게 계산할 수 있다.

예를 들어서, 각 방향별 다음 좌표를 구하기 위해 아래와 같이 direction X / Y 배열을 선언했다고 가정하자.

int[] dirX = {-1, 0, 0, 1};
int[] dirY = {0, -1, 1, 0};

for (int i = 0; i <= 4; i++) {
    int currentX += dirX[i];
    int currentY += dirY[i];
}

직선도로와 커브를 건설하는 케이스는 이 중 어떤 경우일까?

이전 방향이 동 / 서였고 다음 방향이 남 / 북인 경우 또는 이전 방향이 남 / 북이었고 다음 방향이 동 / 서인 경우 2가지라고 볼 수 있겠다. 아래 그림을 한번 참고하자.

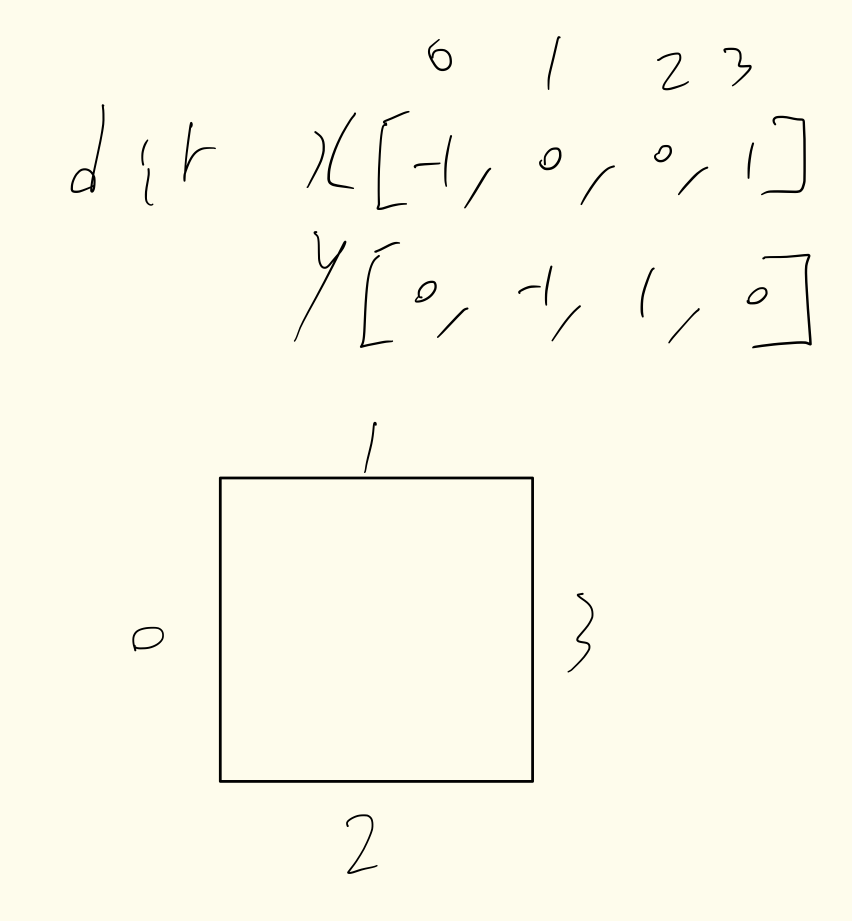
direction

위 형식으로 direction 배열을 구성한 경우, 이전 방향이 0 / 3이었고 다음 방향이 1 / 2일 때 또는 이전 방향이 1 / 2였고 다음 방향이 0 / 3일 때 커브를 건설해야하는 케이스로 볼 수 있다. 해당 케이스에 발생하는 비용은 600원이다.

그렇지 않은 경우는 직선도로만 건설하는 케이스이니, 비용이 100원이다.

위 메서드들을 구현했다면, 푸는 것은 그렇게 어렵지 않을 것이라 예상한다. 하지만 주의할 점이 몇 가지 있으니 그것도 적어보려고 한다.

주의할 점 & TIP

visit 배열 관리

방문 처리한 좌표는 DFS 돌리고 나온 뒤에 다시 false 처리해주는 것을 잊지 말자.

DP 배열 초기값 넣어주기

이 문제는 최소 비용을 구해야 되는 DP 문제이므로, 메모이제이션용으로 사용할 DP 배열에 초기값 채워주는 것을 잊지 말자.

이미 최소값 기록된 좌표에 방문하지 말기

현재 좌표까지의 비용 + 다음 좌표로 건설하는데 드는 비용이 다음 좌표에 기록된 비용보다 큰 경우, 굳이 방문할 필요가 없으며 재방문 하는 경우 오답을 유발할 수 있으니 주의하기 바란다.

이전에 어느 방향에서 왔는지에 따라 비용이 500원씩 달라지기 때문에, 이런 케이스에 대한 예외처리를 해주지 않으면 내가 의도했던 정답이 출력되지 않을 수 있다 😅

게다가 다른 루트를 이용하여 해당 좌표에 더 적은 비용으로 도달했다는 이야기이기도 하므로, 굳이 또 방문할 이유가 없기도 하다.

무슨 말인지 궁금하다면 문제에 주어진 2번 케이스와 4번 케이스를 넣고 돌려보면 된다.

방향별 분기 처리 만들 때는 direction 배열과 for문을 활용하자

이런 류의 문제들은 DFS 재귀 메서드 내부에서 각 방향으로 뻗어나가게 할 때 2가지 방식으로 구현할 수 있다.

// case 1
if (x - 1 >= 0 && x - 1 < size && y >= 0 && y < size) {
    dfs(...)
}

if (x + 1 >= 0 && x + 1 < size && y >= 0 && y < size) {
    dfs(...)
}

if (x >= 0 && x < size && y - 1 >= 0 && y - 1 < size) {
    dfs(...)
}

if (x >= 0 && x < size && y + 1 >= 0 && y + 1 < size) {
    dfs(...)
}

// case 2
int[] dirX = {-1, 0, 0, 1};
int[] dirY = {0, -1, 1, 0};

for (int i = 0; i <= 4; i++) {
    int currentX += dirX[i];
    int currentY += dirY[i];
    dfs(...)
}

어느 방식을 사용하더라도 큰 문제는 없고 개인 취향 차이지만, 개인적으로 case 2 방식을 사용해서 얻는 이득이 많았다. 실수할 확률이 적기도 하고..

꼭 DFS에서만 쓰이는게 아니라 2차원 배열 BFS에서도 쓸 수 있으니 참고 바란다.

전체 코드

전체 코드